3D translation using python in Computer Graphics

Given a line segment where starting point A (32,35) and B point (41,41), and Z (1,3). Apply 3D translation where the translation vector is Tx=1, Ty=3, & Tz=2. and obtain the new co-ordinate & draw the new line.
Theory: In 3D translation, the coordinates of a point x,y,z) can be translated by adding corresponding values from the translation vector Tx,Ty,Tz). The translation operation is given by:
New coordinates=(x+Tx,y+Ty,z+Tz)
Given a line segment with starting point (32,35,0)(32,35,0) and ending point (41,41,0)(41,41,0), and a translation vector (1,3,2)(1,3,2), the new coordinates after translation would be:
New starting point=(32+1,35+3,0+2)=(33,38,2)New starting point=(32+1,35+3,0+2)=(33,38,2)
New ending point=(41+1,41+3,0+2)=(42,44,2)New ending point=(41+1,41+3,0+2)=(42,44,2)
Therefore, the new line segment is formed by connecting the new starting point (33,38,2)(33,38,2) to the new ending point (42,44,2)(42,44,2).

Code:

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

print("Enter the value of x1")
x1 = int(input())
print("Enter the value of x2")
x2 = int(input())
print("Enter the value of y1")
y1 = int(input())
print("Enter the value of y2")
y2 = int(input())
print("Enter the value of z1")
z1 = int(input())
print("Enter the value of z2")
z2 = int(input())

print("Enter the value of Tx")
tx = int(input())
print("Enter the value of Ty")
ty = int(input())
print("Enter the value of Tz")
tz = int(input())

new_x1 = x1 + tx
new_y1 = y1 + ty
new_z1 = z1 + tz

new_x2 = x2 + tx
new_y2 = y2 + ty
new_z2 = z2 + tz

dx = new_x2 - new_x1
dy = new_y2 - new_y1
dz = new_z2 - new_z1

if abs(dx) > abs(dy) and abs(dx) > abs(dz):
    steps = abs(dx)
elif abs(dy) > abs(dz):
    steps = abs(dy)
else:
    steps = abs(dz)

xincrement = dx / steps
yincrement = dy / steps
zincrement = dz / steps

xcoordinate = []
ycoordinate = []
zcoordinate = []

i = 0
while i < steps:
    i += 1
    new_x1 += xincrement
    new_y1 += yincrement
    new_z1 += zincrement
    print("x1:", new_x1, "y1:", new_y1, "z1:", new_z1)
    xcoordinate.append(new_x1)
    ycoordinate.append(new_y1)
    zcoordinate.append(new_z1)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(xcoordinate, ycoordinate, zcoordinate)
ax.set_xlabel("X Axis")
ax.set_ylabel("Y Axis")
ax.set_zlabel("Z Axis")
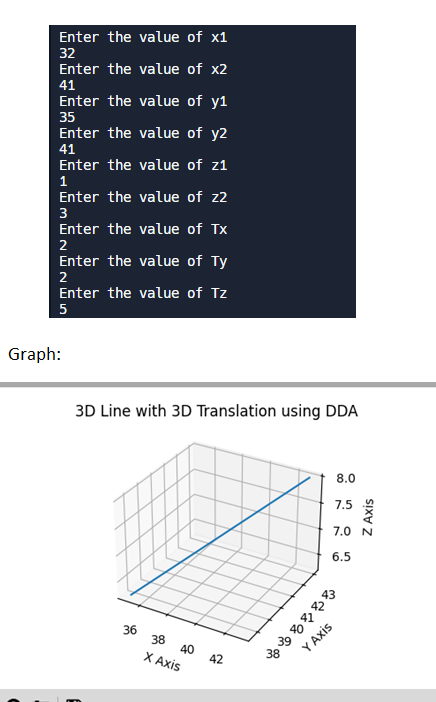
ax.set_title("3D Line with 3D Translation using DDA")
plt.show()