কম্পিউটারের সংখ্যা পদ্ধতি | Number System in Computer (Binary, Octal, Decimal, Hexadecimal)

কম্পিউটারে সংখ্যা পদ্ধতি (Number System in Computer) - ICT Chapter

সূচিপত্র:

• কম্পিউটারের সংখ্যা

• সংখ্যা পদ্ধতির ধারণা

• দশমিক সংখ্যা পদ্ধতি

• বাইনারি সংখ্যা পদ্ধতি

• দশমিক থেকে বাইনারি রূপান্তর

• বাইনারি থেকে দশমিক রূপান্তর

• অক্টাল সংখ্যা পদ্ধতি

• দশমিক থেকে অক্টাল রূপান্তর

• অক্টাল থেকে দশমিক রূপান্তর

• হেক্সাডেসিমেল সংখ্যা পদ্ধতি

• দশমিক থেকে হেক্সাডেসিমেল রূপান্তর

• হেক্সাডেসিমেল থেকে দশমিক রূপান্তর

• বাইনারি সংখ্যার যোগ ও বিয়োগ

• কোডিং: BCD, ASCII ও EBCDIC

কম্পিউটারের সংখ্যা

কম্পিউটার শুধু ০ এবং ১ সংখ্যা বোঝে। এই ০ এবং ১ মূলত বিদ্যুতের উপস্থিতি (১) ও অনুপস্থিতি (০) বোঝাতে ব্যবহৃত হয়। কম্পিউটারে যে কোনো তথ্য, ছবি বা অক্ষরই মূলত বাইনারি (০ ও ১) হিসেবে রূপান্তরিত হয়ে সংরক্ষিত ও প্রক্রিয়াকৃত হয়। বিভিন্ন ধরনের গাণিতিক তথ্য কম্পিউটারে ইনপুট করা যায়। এই সমস্ত তথ্য বোঝার জন্য কম্পিউটারের একটি ভাষা আছে। এবং সেই ভাষাটি ০ এবং ১ এর সমন্বয়ে গঠিত। কম্পিউটার কাজ করে বিদ্যুতের উপস্থিতি এবং অনুপস্থিতি বিবেচনা করে। বিদ্যুতের উপস্থিতি '১' দ্বারা নির্দেশিত হয় এবং অনুপস্থিতিটি '০' দ্বারা নির্দেশিত হয়। বিদ্যুতের উপস্থিতি বা অনুপস্থিতিতে যে বৈদ্যুতিক সংকেত উৎপন্ন হয় তাকে ডিজিটাল সংকেত বলে। বিদ্যুতের উপস্থিতি বা অনুপস্থিতি বুঝতে কম্পিউটার ডিজিটাল সংকেত ব্যবহার করে। কম্পিউটারে যে ধরনের ডেটা দেওয়া হোক না কেন, কম্পিউটার সেটিকে ০ এবং ১ তে রূপান্তর করে। সুতরাং কম্পিউটারের ভিতরে যে সমস্ত ডেটা কাজ করছে তা হল সারি সারি ০ এবং ১। এটি তারপর সমস্ত ০ এবং ১ কে ডিজিটাল সিগন্যালে রূপান্তর করে এবং তারপর বুঝতে পারে প্রয়োজনীয় নির্দেশ বা তথ্য। কম্পিউটারে যেকোনো কাজ এই ০ এবং ১ এর দ্বারা উৎপন্ন ডিজিটাল সিগন্যালের মাধ্যমে সম্পন্ন হয়। তাই ০ এবং ১ কে কম্পিউটারের সংখ্যা পদ্ধতি বলা হয়।

চিত্র: বিদ্যুৎ প্রবাহ ও অনুপস্থিতি (On/Off)

 সংখ্যা পদ্ধতির ধারণা

সংখ্যা বোঝাতে আমরা যে চিহ্ন বা অঙ্ক ব্যবহার করি তাকে সংখ্যা বলা হয়, এবং যেভাবে এ সংখ্যা সাজানো হয় সেটিই সংখ্যা পদ্ধতি (Number System)। প্রতিটি সংখ্যা পদ্ধতির একটি নির্দিষ্ট ভিত্তি বা Base থাকে। কিছু গণনা করার চেষ্টা করা থেকেই মানুষ সংখ্যার আবিষ্কার করতে পেরেছে। চিহ্ন গুলি কোনো কিছু গণনা এবং রেকর্ড রাখতে ব্যবহার করা হয়। উদাহরণস্বরূপ- ১, ২, ৩ ইত্যাদি এই চিহ্নগুলি ধারা সংখ্যা প্রকাশ করা হয়। আমরা যে গণিত করি তা এই চিহ্ন বা সংখ্যা ব্যবহার করে সাথে নিয়ে কাজ করি। এই সংখ্যাগুলোকে পাশাপাশি লিখে প্রকাশ করার পদ্ধতিকে সংখ্যা পদ্ধতি বলে। উদাহরণস্বরূপ, ১(এক) এবং ০ (শূন্য) পাশাপাশি লেখা মানে ১০(দশ) আবার ১(এক) এবং ১ (এক) সাথে নিয়ে লেখলে আমরা ১১ (এগারো) বুঝি। আমরা সাধারণত যে সংখ্যা পদ্ধতি ব্যবহার করি তাকে বলা হয় দশমিক সংখ্যা পদ্ধতি। কম্পিউটার যে সংখ্যা পদ্ধতি ব্যবহার করে তাকে বাইনারি সংখ্যা পদ্ধতি বলে। এরকম আরো অনেক সংখ্যা পদ্ধতি আছে।

প্রধান সংখ্যা পদ্ধতিসমূহ:

1. দশমিক (Decimal) – ভিত্তি ১০ (০-৯)

2. বাইনারি (Binary) – ভিত্তি ২ (০, ১)

3. অক্টাল (Octal) – ভিত্তি ৮ (০-৭)

4. হেক্সাডেসিমেল (Hexadecimal) – ভিত্তি ১৬ (০ থেকে ১৬ পর্যন্ত- ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯, ০, A, B, C, D, E এবং F)।

দশমিক সংখ্যা পদ্ধতি

আমাদের দৈনন্দিন জীবনে ব্যবহৃত সংখ্যা পদ্ধতি হল দশমিক। এটি ১০টি অঙ্ক (০-৯) নিয়ে গঠিত। কম্পিউটারে আমরা যখন কিছু লিখি, তা দশমিক আকারে হলেও কম্পিউটার একে বাইনারিতে রূপান্তর করে কাজ করে। আমরা জানি যে গণিত লেখা কিছু চিহ্ন বা সংখ্যার সাহায্যে করা হয়। যাইহোক, আমরা যে পদ্ধতিতে সংখ্যা লিখি তার উপর নির্ভর করে কতগুলো চিহ্ন বা সংখ্যা লেখা যাবে তা জানা যাই। আমরা সাধারণত যে পদ্ধতিতে সংখ্যা লিখি তাতে দশটি চিহ্ন বা অক্ষর ব্যবহার করা হয়, তাই একে দশমিক পদ্ধতি বলা হয়। অর্থাৎ, দশমিক পদ্ধতিতে ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯, ০ দশটি সংখ্যা থাকে। এই পদ্ধতিতে লেখা সংখ্যার ভিত্তি হল ১০। এভাবে ১, ২, ৩, ৪, ৫ ইত্যাদির উপর ভিত্তি করে সংখ্যা লেখা যায়। তবে দশ ভিত্তিক সংখ্যার প্রচলন সবচেয়ে বেশি। অন্য কোন উপায়ে লেখা একটি সংখ্যার মান বোঝার জন্য, আমরা এটিকে প্রথমে দশ ভিত্তিক সংখ্যায় রূপান্তর করে নেই। কারণ, আমরা ছোটবেলা থেকেই দশ ভিত্তিক সংখ্যা পরে এসেছি। আমরা যখন কম্পিউটারে একটি সংখ্যা লিখি, তখন আমরা সেটিকে দশমিক আকারে লিখি। কম্পিউটার কিন্তু এই পদ্ধতি সরাসরি বুঝতে পারে না। কম্পিউটার বাইনারি নম্বর সিস্টেম বোঝে। ফলস্বরূপ, কম্পিউটার দশমিক সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর করে এবং প্রক্রিয়াকরণের পরে এটিকে আবার রূপান্তর করে আমাদের দশমিক সংখ্যায় ফলাফল দেয়।

দশমিক সংখ্যা পদ্ধতি আমাদের দৈনন্দিন জীবনে সবচেয়ে বহুল ব্যবহৃত সংখ্যা পদ্ধতি। এটি ১০ ভিত্তিক (Base-10) সংখ্যা পদ্ধতি, যার মধ্যে ০ থেকে ৯ পর্যন্ত মোট ১০টি অঙ্ক ব্যবহৃত হয়। প্রতিটি সংখ্যার একটি নির্দিষ্ট স্থানীয় মান (Place Value) থাকে এবং প্রতিটি স্থানে ব্যবহৃত সংখ্যাটি ১০ এর ঘাত অনুযায়ী গুণ করা হয়।

উদাহরণস্বরূপ: 452 = (4×10²) + (5×10¹) + (2×10⁰) = 400 + 50 + 2 = 452

দশমিক পদ্ধতির বৈশিষ্ট্য হলো এটি একটি পজিশনাল (Positional) সিস্টেম, অর্থাৎ সংখ্যা লেখার প্রতিটি অঙ্কের মান তার অবস্থানের ওপর নির্ভর করে। এই পদ্ধতির কারণেই আমরা খুব সহজে বড় সংখ্যাগুলো প্রকাশ করতে পারি।

বাইনারি সংখ্যা পদ্ধতি

বাইনারি পদ্ধতিতে মাত্র দুটি সংখ্যা ব্যবহৃত হয় — ০ এবং ১। কম্পিউটার এই পদ্ধতির মাধ্যমেই সকল গাণিতিক ও লজিকাল কাজ সম্পাদন করে। ০ এবং ১ এ দুই অঙ্কের সংখ্যা পদ্ধতিকে বাইনারি সংখ্যা পদ্ধতি বলা হয়। বাইনারি হল সবচেয়ে সহজ সংখ্যা পদ্ধতি। এর ভিত্তি হল ২। ০ এবং ১ চিহ্ন দুটিকে গণিতের ভাষায় সংখ্যা বলা হয়। মাত্র দুটি চিহ্ন বা সংখ্যা দিয়ে সংখ্যা লেখার এই পদ্ধতি বাইনারি পদ্ধতি নামে পরিচিত। তাই এই দুটি সংখ্যাকে বাইনারি সংখ্যা বা বাইনারি অংক বলা হয়। কম্পিউটার বাইনারি সংখ্যার সাহায্যে সব ধরনের গণনা বা যেকোনো কাজ করে থাকে। বাইনারি সংখ্যা দ্বারা গঠিত কম্পিউটার ভাষাকে বাইনারি ভাষা বলে। আর বাইনারি সংখ্যার বিভিন্ন গাণিতিক প্রক্রিয়াকে বলা হয় বাইনারি গণিত বা কম্পিউটার গণিত। আমরা সাধারণত যে সংখ্যাটি ব্যবহার করি তা দশটি একক নিয়ে গঠিত। ০ থেকে ৯ কে একটি একক দশমিক(১০) দ্বারা প্রকাশ করা যায়। কিন্তু যখনই সংখ্যাটি ৯ এর বেশি হবে, তখনই বাম দিকে এক সংখ্যাটি লাগাতে হবে অথ্যাৎ ১০। একইভাবে বাইনারি সিস্টেমে দুটি ইউনিট রয়েছে যথা, ০ এবং ১। সাধারণ সংখ্যায় যেকোন ৯ এর বেশি হয়, তখন আপনাকে এটিকে বাম দিকে বাড়াতে হয় টিক তেমনি বাইনারি সিস্টেমের সময়ও আপনাকে বাম দিক থেকে বাড়াতে হবে।

বাইনারি সংখ্যা পদ্ধতি হল কম্পিউটারের ভাষা। এটি মাত্র দুটি সংখ্যা নিয়ে গঠিত — ০ এবং ১, এবং এর ভিত্তি (Base) হল ২। কম্পিউটার সকল ডেটা ও নির্দেশনা এই ০ ও ১ এর মাধ্যমে বুঝে এবং প্রক্রিয়া করে।

বাইনারি সংখ্যা সাধারণত ডিজিটাল সার্কিটের 'চালু' (On = 1) এবং 'বন্ধ' (Off = 0) অবস্থার সাথে সম্পর্কিত।

উদাহরণস্বরূপ: 1011 (বাইনারি) = (1×2³) + (0×2²) + (1×2¹) + (1×2⁰) = 8 + 0 + 2 + 1 = 11 (দশমিক)

চিত্র: বাইনারি মান নির্ধারণ

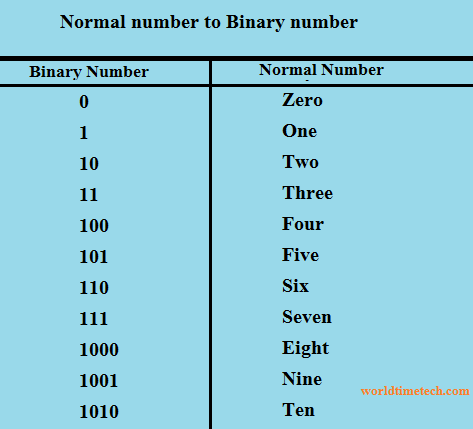
এখানে লক্ষ্য করা যায় যে বাইনারি সিস্টেমে সর্বাধিক সংখ্যা হল ১। এর উপরে হলেই, বাম দিকের সংখ্যাই এক সংখ্যা বৃদ্ধি পায়। তাই এই পদ্ধতিতে ০ মানে শূন্য এবং ১ মানে এক। কিন্তু ১০ মানে দুই। বাইনারি সিস্টেমে আমরা বামে একটি সংখ্যা যোগ করি কারণ ১ এর উপরে কোন সংখ্যা নেই।

নীচে বাইনারি এবং দশমিক পদ্ধতির মধ্যে তুলনা করা হল।
চিত্র: বাইনারি ও দশমিক তুলনা

 

দশমিক থেকে বাইনারি রূপান্তর

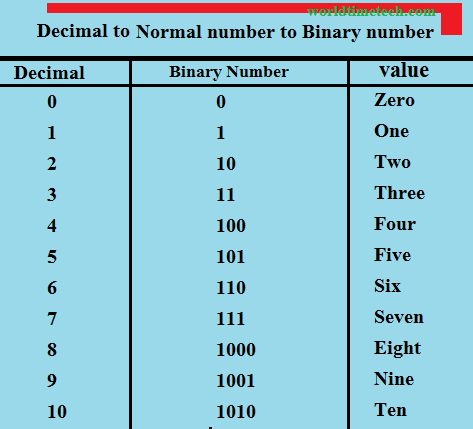
একটি দশমিক সংখ্যাকে দুই দিয়ে ভাগ করতে থাকলে এবং ভাগশেষগুলো উল্টোভাবে সাজালে বাইনারি সংখ্যা পাওয়া যায়। 

আসুন এখন জানি কিভাবে একটি দশমিক সংখ্যাকে বাইনারি সংখ্যায় রূপান্তর করা যায়। দশমিককে বাইনারিতে রূপান্তর করার সবচেয়ে সহজ উপায় হল দশমিক সংখ্যাকে দুই দ্বারা ভাগ করা। এবং ভাগশেষগুলোকে পাশাপাশি সাজালেই সমতুল্য বাইনারি সংখ্যা পাওয়া যাবে। এখানে শেষ অবশিষ্ট সংখ্যাগুলোকে সর্বোচ্চ গুরুত্ব সংখ্যা হিসেবে নেওয়া হয়েছে।

একটি দশমিক পূর্ণসংখ্যাকে বাইনারিতে রূপান্তরের সবচেয়ে সহজ উপায় হল সংখ্যাটিকে ২ দ্বারা ভাগ করে ক্রমানুসারে ভাগশেষগুলো সংগ্রহ করা। এই ভাগশেষগুলো উল্টোভাবে (শেষ থেকে শুরু করে) সাজালেই বাইনারি সংখ্যা পাওয়া যায়।

উদাহরণ: ১০ (দশমিক)
10 ÷ 2 = 5, ভাগশেষ = 0
5 ÷ 2 = 2, ভাগশেষ = 1
2 ÷ 2 = 1, ভাগশেষ = 0
1 ÷ 2 = 0, ভাগশেষ = 1
ফলাফল: 1010 (বাইনারি)

একইভাবে ভগ্নাংশ দশমিক সংখ্যাকেও গুণফল পদ্ধতিতে বাইনারিতে রূপান্তর করা যায়, যেখানে বারবার ২ দ্বারা গুণ করা হয় এবং পূর্ণ সংখ্যাগুলো আলাদা করে নেওয়া হয়।

উদাহরণ: চলুন ২৫ (দশমিক) সংখ্যাটিকে বাইনারিতে রূপান্তর করি।

চিত্র: ২৫ → বাইনারি (১১০০১)

 

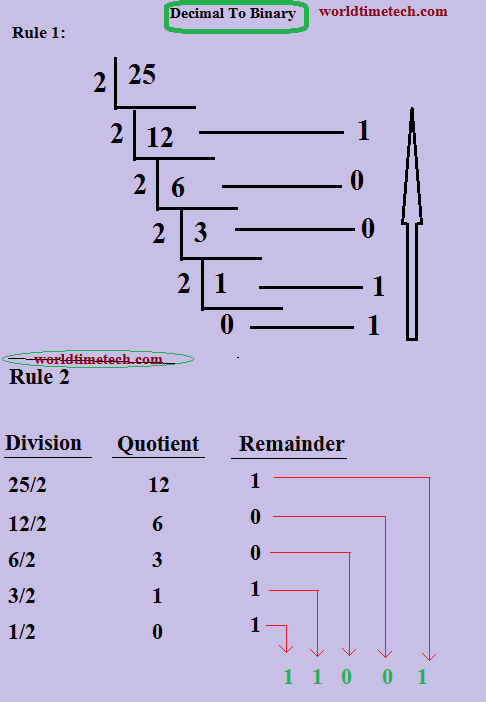
ফলাফল ১১০০১(পঁচিশ) বাইনারি

আপনি এ দুটি নিয়ম থেকে যেকোনো একটি করবেন।

একটি ভগ্নাংশ দশমিক সংখ্যাকে বাইনারিতে রূপান্তর করতে, আপনাকে এটিকে দুই দ্বারা গুণ করতে হবে। প্রাপ্ত ফলাফলের ভগ্নাংশকে বারবার গুণ করতে হবে যতক্ষণ না পূণ সংখ্যায় পৌঁছায়। বাছাইকৃত সমতুল্য বাইনারি সংখ্যার পাশাপাশি সাজালে ফলাফলের বাইনারি সংখ্যা পাওয়া যাবে। এই ক্ষেত্রে, প্রথম পূর্ণ সংখ্যাটি সর্বোচ্চ গুক্তত্বেও সংখ্যা হিসাবে বিবেচিত হয়।

উদাহরণস্বরূপ, আসুন ৩৫ নম্বরটিকে একটি বাইনারি সংখ্যায় রূপান্তর করি।

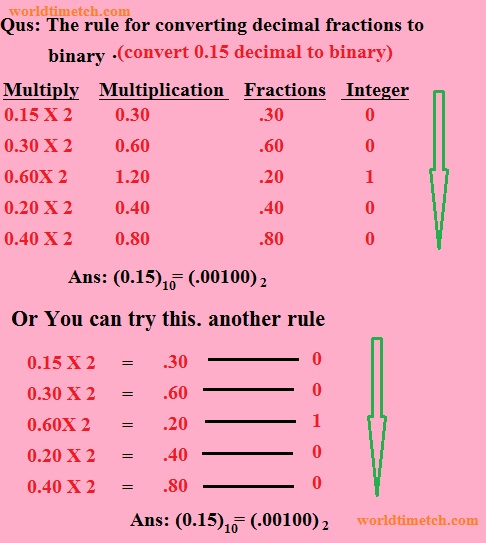
ফলাফল: ১৫ দশমিক = . ০০১০০ আসন্ন মান।
 

বাইনারি থেকে দশমিক রূপান্তর

বাইনারি সংখ্যার প্রতিটি অংককে তার স্থানীয় মান অনুযায়ী গুণ করে যোগ করলেই দশমিক সংখ্যা পাওয়া যায়। 

আমরা একটি সংখ্যার স্থানীয় মান দিয়ে গুণ করে তার মোট মান খুঁজে পেতে পারি। যেমন একক, দশক, শতাব্দী, স্থানীয় মান এইভাবে পাওয়া যাবে। তবে বাইনারি সংখ্যাগুলিকে তাদের স্থানীয় মানগুলিকে গুণ করে এবং প্রাপ্ত মানগুলি যোগ করে দশমিক সংখ্যায় রূপান্তর করা যেতে পারে।

বাইনারি সংখ্যাকে দশমিক সংখ্যায় রূপান্তর করতে, প্রতিটি বাইনারি অঙ্ককে তার অবস্থান অনুযায়ী ২ এর ঘাত দ্বারা গুণ করতে হয় এবং সবগুলো মানকে যোগ করতে হয়।

উদাহরণ: 1101 (বাইনারি)
= (1×2³) + (1×2²) + (0×2¹) + (1×2⁰)
= 8 + 4 + 0 + 1 = 13 (দশমিক)

ভগ্নাংশযুক্ত বাইনারি সংখ্যার ক্ষেত্রেও একই নিয়ম অনুসরণ করে দশমিক মান নির্ধারণ করা হয়। যেমন .101 = (1×2⁻¹) + (0×2⁻²) + (1×2⁻³) = 0.5 + 0 + 0.125 = 0.625 (দশমিক)

নীচে সংখ্যাটি ১১০০১ (বাইনারী পঁচিশ) দশমিক সংখ্যায় রূপান্তরিত হয়েছে।

চিত্র: ১১০০১ → দশমিক (২৫)


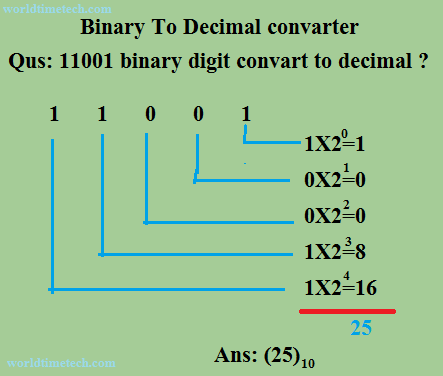
আপনি যদি একটি বাইনারি সংখ্যার একটি ভগ্নাংশকে দশমিক সংখ্যায় রূপান্তর করতে চান, আপনি ফলাফলটিকে তার স্থানীয় মান দ্বারা গুণ করতে পারেন এবং গুণফলটিকে যোগ করলে দশমিক সমতুল্য সংখ্যা পারেন। উদাহরণস্বরূপ, আসুন .১০১০ সংখ্যাটিকে দশমিক সংখ্যায় রূপান্তর করি।

অক্টাল সংখ্যা পদ্ধতি

বাইনারি সংখ্যার তুলনায় সংক্ষিপ্ত ও সহজবোধ্য হওয়ায় কম্পিউটারে অক্টাল সংখ্যা ব্যবহৃত হয়। এটির ভিত্তি ৮ এবং সংখ্যা ০ থেকে ৭। বাইনারি সংখ্যাগুলিকে বেশ দীর্ঘ হয় তাই অক্টাল সংখ্যা পদ্ধতির উদ্ভব হয়েছে যা এটিকে সহজ এবং সংক্ষিপ্ত আকারে উপস্থাপন করে। এই নম্বর সিস্টেমটি কম্পিউটারের অভ্যন্তরীণ বাইনারি সংখ্যাগুলি প্রক্রিয়া করতে ব্যবহৃত হয়। অক্টাল সংখ্যা পদ্ধতির ভিত্তি হল আট। অক্টাল সংখ্যা পদ্ধতিতে ৮টি সংখ্যা রয়েছে। এগুলি হল ০, ১, ২, ৩, ৪, ৫, ৬ এবং ৭ যার মানে এখানে সবচেয়ে বড় সংখ্যা হল ৭। এবং এর চেয়ে একটি বড় সংখ্যা গঠন করতে, আপনাকে দুই বা তার বেশি সংখ্যা বিন্যাস করতে হবে। নীচের টেবিলটি দশমিক সংখ্যার পাশাপাশি বাইনারি সমতুল্য সংখ্যাগুলি দেখায়।

চিত্র: দশমিক ও বাইনারি সমতুল্য

 

অক্টাল সংখ্যা পদ্ধতি একটি ৮ ভিত্তিক (Base-8) সংখ্যা পদ্ধতি। এতে ০ থেকে ৭ পর্যন্ত মোট ৮টি অঙ্ক ব্যবহার করা হয়। অর্থাৎ, অক্টাল সংখ্যায় শুধুমাত্র ০, ১, ২, ৩, ৪, ৫, ৬, এবং ৭ অঙ্কগুলোই ব্যবহৃত হতে পারে।

কম্পিউটারে মেমোরি অ্যাড্রেস ও পারমিশন সিস্টেম বোঝাতে অক্টাল সংখ্যা পদ্ধতি অনেক সময় ব্যবহৃত হয়। বাইনারি সংখ্যাকে সহজভাবে প্রকাশ করতে অক্টাল পদ্ধতি সহায়ক হিসেবে কাজ করে, কারণ প্রতিটি ৩টি বাইনারি বিটকে একটি অক্টাল সংখ্যায় রূপান্তর করা যায়।

উদাহরণস্বরূপ: অক্টাল সংখ্যা 725 এর মান
= (7×8²) + (2×8¹) + (5×8⁰) = 448 + 16 + 5 = 469 (দশমিক)

দশমিক ↔ অক্টাল রূপান্তর

দশমিক সংখ্যাকে ৮ দিয়ে ভাগ করলে অক্টাল সংখ্যা পাওয়া যায়। যেহেতু অক্টাল সংখ্যার ভিত্তি আট। সুতরাং যেকোনো দশমিক পূর্ণ সংখ্যাকে আট দ্বারা ভাগ করে অক্টাল সংখ্যায় রূপান্তর করা যেতে পারে। ভাগফল শূন্য না হওয়া পর্যন্ত পুনঃবন্টন করতে হবে এবং ভাগফলকে পাশাপাশি সাজিয়ে অক্টাল সংখ্যা পাওয়া যাবে। এখানে শেষ অংশটি সর্বোচ্চ গুক্তত্বের সংখ্যা হিসাবে বিবেচিত হবে। উদাহরণস্বরূপ, আসুন ৭৫ (দশমিক) সংখ্যাটিকে একটি অক্টাল সংখ্যায় রূপান্তর করি।
চিত্র: ৭৫ → অক্টাল


আপনি যদি একটি দশমিক ভগ্নাংশ সংখ্যাকে অক্টাল সংখ্যায় রূপান্তর করতে চান তবে আপনাকে সেই সংখ্যাটিকে আট দ্বারা গুণ করতে হবে এবং পূর্ণ সংখ্যাটি আলাদা করতে হবে। যদি গুণফলে ভগ্নাংশ থাকে তবে এটিকে আবার গুণ করতে হবে। সবশেষে, পূর্ণ সংখ্যাগুলো পাশাপাশি সাজানো হলে অক্টাল সংখ্যা পাওয়া যায়। এক্ষেত্রে প্রথম পূর্ণ সংখ্যাটিকে সর্বোচ্চ গুক্তত্বে সংখ্যা হিসেবে ধরা হয়। উদাহরণস্বরূপ, আসুন 0.২৫ কে একটি অক্টাল সংখ্যায় রূপান্তর করি।

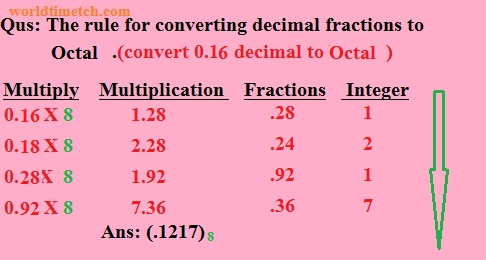
একটি দশমিক সংখ্যাকে অক্টালে রূপান্তর করতে হলে সংখ্যাটিকে বারবার ৮ দিয়ে ভাগ করতে হয় এবং প্রতিবারের ভাগশেষ (remainder) নিচ থেকে ওপরে উল্টোভাবে সাজালে অক্টাল সংখ্যা পাওয়া যায়।

উদাহরণ: 83 (দশমিক) কে অক্টালে রূপান্তর:
83 ÷ 8 = 10, ভাগশেষ = 3
10 ÷ 8 = 1, ভাগশেষ = 2
1 ÷ 8 = 0, ভাগশেষ = 1
অতএব, 83 = 123 (অক্টাল)

ভগ্নাংশ দশমিক সংখ্যার ক্ষেত্রেও ৮ দ্বারা গুণ করে পূর্ণ সংখ্যা সংগ্রহের মাধ্যমে অক্টাল রূপ পাওয়া যায়।

অক্টাল থেকে দশমিক সংখ্যায় রূপান্তর

অক্টাল সংখ্যা একইভাবে তার স্থানীয় মান দ্বারা গুণিত করে এবং পরে গুণফল দ্বারা যোগ করলে দশমিক সংখ্যায় রূপান্তর হয়। নিচের উদাহরণটি লক্ষ্য করুন। ১১৩.১২ অক্টাল সংখ্যাটি দশমিক সংখ্যায় রূপান্তরিত।
অক্টাল → দশমিক রূপান্তরের জন্য স্থানীয় মান ব্যবহার করে গুণ করতে হয়।
চিত্র: ১১৩.১২ অক্টাল → দশমিক

অক্টাল সংখ্যাকে দশমিক রূপে প্রকাশ করার জন্য প্রতিটি অঙ্ককে তার অবস্থান অনুযায়ী ৮ এর ঘাত দ্বারা গুণ করতে হয় এবং সবগুলো গুণফল যোগ করতে হয়।

উদাহরণ: 146 (অক্টাল)
= (1×8²) + (4×8¹) + (6×8⁰)
= 64 + 32 + 6 = 102 (দশমিক)

ভগ্নাংশ যুক্ত অক্টাল সংখ্যার ক্ষেত্রেও একই নিয়ম প্রযোজ্য। যেমন:
অক্টাল: 0.52 = (5×8⁻¹) + (2×8⁻²) = 0.625 + 0.03125 = 0.65625 (দশমিক)

 হেক্সাডেসিমেল সংখ্যা পদ্ধতি

এই পদ্ধতিতে ১৬টি চিহ্ন ব্যবহৃত হয়: ০-৯ এবং A-F (A=10, B=11, ..., F=15)। কম্পিউটারে বড় সংখ্যাগুলো সংক্ষেপে প্রকাশের জন্য হেক্সাডেসিমেল ব্যবহৃত হয়। কম্পিউটারে ব্যবহৃত আরেকটি সংখ্যা পদ্ধতিকে বলা হয় হেক্সাডেসিমেল সংখ্যা পদ্ধতি। এই নম্বর সিস্টেমটি কম্পিউটারের অভ্যন্তরীণ বাইনারি সংখ্যাগুলি প্রক্রিয়া করতেও ব্যবহৃত হয়। হেক্সাডেসিমেল হল একটি ১৬ ভিত্তিক সংখ্যা পদ্ধতি। এই পদ্ধতিতে ১৬টি চিহ্ন, প্রতীক বা সংখ্যা রয়েছে। এগুলি হল ০, ১, ২, ৩, ৪, ৫, ৬, ৭, ৮, ৯, A, B, C, D, E এবং F৷ নীচের টেবিলটি দশমিক সংখ্যার পাশাপাশি হেক্সাডেসিমেল সমতুল্য সংখ্যাগুলিও দেখানো হলো৷

চিত্র: হেক্সাডেসিমেল টেবিল

হেক্সাডেসিমেল সংখ্যা পদ্ধতি একটি ১৬ ভিত্তিক (Base-16) সংখ্যা পদ্ধতি, যার মাধ্যমে ০ থেকে ১৫ পর্যন্ত মান প্রকাশ করা যায়। এই পদ্ধতিতে ০ থেকে ৯ পর্যন্ত দশটি সংখ্যা এবং অতিরিক্ত ছয়টি বর্ণ (A-F) ব্যবহার করা হয়। যেখানে:

• 10 = A
• 11 = B
• 12 = C
• 13 = D
• 14 = E
• 15 = F

হেক্সাডেসিমেল সংখ্যা পদ্ধতি মূলত কম্পিউটার সিস্টেমে রঙ নির্ধারণ, মেমোরি অ্যাড্রেসিং এবং বিটের বড় মান সহজভাবে প্রকাশ করতে ব্যবহৃত হয়। কারণ, প্রতিটি হেক্সাডেসিমেল অঙ্ক ৪টি বাইনারি বিট প্রকাশ করে।

উদাহরণস্বরূপ: 2F3 (Hexadecimal) = (2×16²) + (F×16¹) + (3×16⁰) = 512 + 240 + 3 = 755 (দশমিক)

 দশমিক ↔ হেক্সাডেসিমেল রূপান্তর

দশমিক সংখ্যাকে ১৬ দিয়ে ভাগ করে হেক্সাডেসিমেল রূপে পাওয়া যায়। 

হেক্সাডেসিমেল সংখ্যার ভিত্তি হল ১৬৷ একটি পূর্ণ দশমিক সংখ্যাকে একটি হেক্সাডেসিমেল সংখ্যায় রূপান্তর করতে, এটিকে ১৬ দ্বারা ভাগ করতে হবে৷ ভাগফলটি শূন্য না হওয়া পর্যন্ত পুনরায় ভাগ করতে হবে৷ সবশেষে, ভাগশেষসমূহ শেষ থেকে শুরুতে অবশিষ্টাংশকে বাছাই করলে হেক্সাডেসিমেল সংখ্যা পাওয়া যায়।

৫৫ দশমিক সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর করা যাক।

চিত্র: ৫৫ → ৩৭ (Hex)

ফলাফল: ৩৭ (পঞ্চান্ন - হেক্সাডেসিমেল সংখ্যা পদ্ধতি)।

আপনি যদি একটি দশমিক ভগ্নাংশ সংখ্যাকে হেক্সাডেসিমেল সংখ্যায় রূপান্তর করতে চান তবে আপনাকে পুনঃ পুনঃ ১৬ দ্বারা ভগ্নাংশকে গুণ করতে হবে। গুণফল থেকে প্রাপ্ত পূর্ণসংখ্যাগুলি পাশাপাশি সাজিয়ে হেক্সাডেসিমেল সংখ্যা পাওয়া যায়। উদাহরণস্বরূপ, আসুন আমরা ০.৫০ সংখ্যাটিকে একটি হেক্সাডেসিমেল সংখ্যায় রূপান্তর করি।

চিত্র: ০.৫০ → ০.৮ (Hex)


ফলাফল: ০.৮ হেক্সাডেসিমেল

দশমিক সংখ্যা থেকে হেক্সাডেসিমেল রূপান্তরের জন্য সংখ্যাটিকে ১৬ দ্বারা ভাগ করতে হয় এবং প্রতিবারের ভাগশেষগুলো নিচ থেকে ওপরে (উল্টোভাবে) সাজাতে হয়। ১০ থেকে ১৫ পর্যন্ত ভাগশেষ থাকলে সেগুলোকে A থেকে F দ্বারা প্রকাশ করা হয়।

দশমিক থেকে হেক্সাডেসিমেল রূপান্তর

উদাহরণ: 254 (দশমিক)
254 ÷ 16 = 15, ভাগশেষ = 14 → E
15 ÷ 16 = 0, ভাগশেষ = 15 → F
ফলাফল: 254 = FE (Hexadecimal)

ভগ্নাংশ সংখ্যার ক্ষেত্রেও ১৬ দ্বারা গুণ করে হেক্সাডেসিমেল মান নির্ধারণ করা যায়।

হেক্সাডেসিমেল থেকে দশমিক সংখ্যায় রূপান্তর

হেক্সাডেসিমেল সংখ্যার ভিত্তি হল ১৬। আপনি যদি একটি হেক্সাডেসিমেল সংখ্যাকে দশমিক সংখ্যায় রূপান্তর করতে চান, আপনি সেই সংখ্যাটিকে তার স্থানীয় মান দ্বারা গুণ করতে পারেন এবং প্রাপ্ত সংখ্যাগুলি যোগ করলে দশমিক সংখ্যা পাবেন।

A২.৮ কে হেক্সাডেসিমেল সংখ্যাকে দশমিক সংখ্যায় রূপান্তর ।

 বাইনারি সংখ্যার যোগ ও বিয়োগ

কম্পিউটার মূলত এই বাইনারি সিস্টেমে কাজ করে। যেকোনো অক্ষরগুলি এই বাইনারি সংখ্যায় রূপান্তরিত হয়। বাইনারি সংখ্যাটি তখন বৈদ্যুতিক কম্পনে রূপান্তরিত হয়। তাই এই বাইনারি সংখ্যার মাধ্যমে বিদ্যুতের উপস্থিতি ও অনুপস্থিতি তুলে ধরা যায়।

নীচে বাইনারি পদ্ধতিতে যোগ এবং বিয়োগের জন্য দুটি টেবিল রয়েছে।

চিত্র: বাইনারি যোগ টেবিল

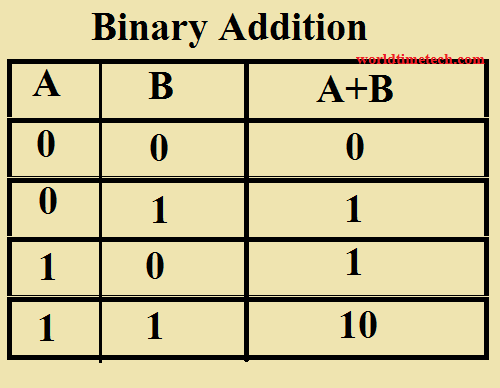
বাইনারি যোগের চারটি মূল নিয়ম:

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 10 (যেখানে ০ আসে এবং ১ ক্যারি হয়)

উদাহরণস্বরূপ:
    1011
+  1101
= 11000

চিত্র: বাইনারি বিয়োগ টেবিল

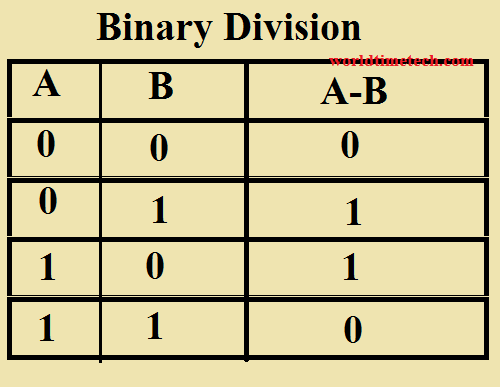
বাইনারি বিয়োগ (Binary Subtraction)

বাইনারি বিয়োগেও চারটি মৌলিক নিয়ম আছে:

• 0 - 0 = 0
• 1 - 0 = 1
• 1 - 1 = 0
• 0 - 1 = 1 (এক্ষেত্রে ১ ধার নিতে হয়)

উদাহরণস্বরূপ:
    1010
-   0011
= 0111

কমপ্লিমেন্ট পদ্ধতির মাধ্যমেও বাইনারি বিয়োগ সম্পাদন করা যায়, যেমন: ১’স কমপ্লিমেন্ট বা ২’s কমপ্লিমেন্ট ব্যবহার করে।

হেক্সাডেসিমেল সংখ্যাকে দশমিক রূপে প্রকাশ করতে হলে, প্রতিটি অঙ্ককে তার অবস্থান অনুসারে ১৬ এর ঘাত দ্বারা গুণ করতে হয় এবং সব গুণফল যোগ করতে হয়। A থেকে F পর্যন্ত বর্ণগুলোর মান যথাক্রমে 10 থেকে 15 পর্যন্ত ধরে নিতে হয়।

উদাহরণ: 1A3 (Hexadecimal)
= (1×16²) + (A×16¹) + (3×16⁰)
= 1×256 + 10×16 + 3×1 = 256 + 160 + 3 = 419 (দশমিক)

ভগ্নাংশযুক্ত হেক্সাডেসিমেল সংখ্যার ক্ষেত্রেও একই নিয়মে ১৬ এর ঋণাত্মক ঘাত ব্যবহার করে দশমিক মান বের করা হয়। যেমন:
Hex: 0.F = (15×16⁻¹) = 0.9375 (দশমিক)

 কোডিং ও ডেটা রূপান্তর

কম্পিউটার ইনপুট হিসেবে আসা অক্ষর, সংখ্যা বা চিহ্নগুলোকে বাইনারিতে রূপান্তর করে নেয়। এই প্রক্রিয়াকে বলা হয় কোডিং। আমরা কম্পিউটারে দশমিক সংখ্যা ইনপুট করি। কিন্তু কম্পিউটার সরাসরি নম্বর বুঝতে পারে না। কারণ কম্পিউটার বাইনারি সংখ্যা বুঝতে পারে। তাই কম্পিউটারে বর্ণ, সংখ্যা, চিহ্ন, চিহ্ন ইত্যাদি ইনপুট সমতুল্য বাইনারি সংখ্যায় রূপান্তরিত করে নেয়া হয়। রূপান্তর প্রক্রিয়াকে কোডিং বলা হয়। যখন বড় দশমিক সংখ্যাগুলি বাইনারি সংখ্যায় লেখা হয়, তখন অনেক বড় হয়ে যায়। উদাহরণস্বরূপ, আপনি যদি ৩২৭৬৭ নম্বরটি বাইনারিতে লিখতে চান তবে এটি হবে ১১১১১১১১১১১১১১। তারপর এক লাখ বা ​​এক কোটি প্রকাশ করার জন্য প্রচুর বাইনারি সংখ্যার সংখ্যা প্রয়োজন। এই কারণে, ৯ দশমিকের বেশি সংখ্যাগুলিকে কোড করা হয় । দশমিক ০-৯ পর্যন্ত দশ সংখ্যার বাইনারি কোড মনে রাখার মাধ্যমে যেকোন বড় সংখ্যক কোড সহজেই নির্ধারণ করা সম্ভব।

BCD (Binary Coded Decimal)

BCD কোড ব্যবহার করে প্রতিটি দশমিক অংককে পৃথক ৪-বিট বাইনারি সংখ্যায় রূপান্তর করা হয়। বাইনারি কোডেড ডেসিমেল (BCD) কোড তৈরি করা হয়েছে দশমিক সংখ্যাকে বাইনারি সংখ্যায় বা বাইনারি সংখ্যাকে দশমিক সংখ্যায় রূপান্তর করার প্রক্রিয়া সহজতর করার জন্য। ৮ বিট কোড প্রকাশের জন্য স্ট্যান্ডার্ড মান হিসাবে বিবেচিত হয়। যাইহোক, ০-৯ পর্যন্ত সংখ্যা প্রকাশ করার জন্য শুধুমাত্র ৪ বিট যথেষ্ট। বাকি চারটির মধ্যে তিনটিকে বলা হয় জোন বিট এবং অন্যটিকে প্যারিটি বিট। জটিলতা এড়াতে ৮ বিটের পরিবর্তে ৪ বিট বিসিডি কোডের উদাহরণ দেওয়া হলো: উদাহরণ:
BCD টেবিল


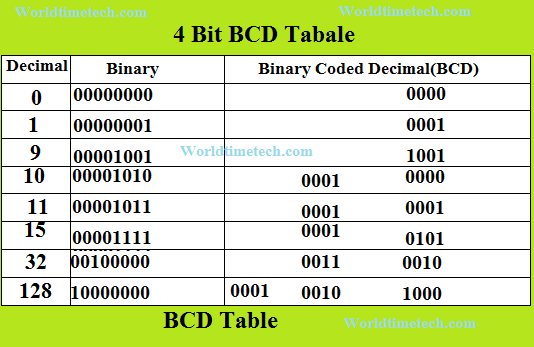
শেষ উদাহরণ বিশ্লেষণ করা যাক, ১২৮ দশমিক নম্বরটি বাইনারিতে প্রকাশ করতে ৮ বিট প্রয়োজন, যা বাইনারিতে ১০০০০০০০ হবে এবং BCD কোডে ৪ বিট প্রকাশ করতে ১,২ এবং ৮কে আলাদাভাবে ৪ বিট বাইনারি কোডে লিখতে হবে। এইভাবে ০-৯ পর্যন্ত ৪ বিট বাইনারি কোড ব্যবহার করে যেকোনো বড় সংখ্যাকে সহজেই প্রকাশ করা যায়। ০-১৫ পর্যন্ত মোট ষোলটি বাইনারি সংখ্যা ৪ বিট ব্যবহার করে প্রকাশ করা যেতে পারে। কিন্তু BCD কোডে শুধুমাত্র ০-৯ বাইনারি ফরম্যাট ব্যবহার করা হয়। অবশিষ্ট ১০১০,১০১১,১১০০, ১১০১,১১১০ এবং ১১১১ মোট ছয়টি ফরম্যাট ব্যবহার করা হয়েছে। বিসিডি কোডগুলি ক্যালকুলেটর, ইলেকট্রনিক কাউন্টার, ডিজিটাল ভোল্টমিটার, ডিজিটাল ঘড়ি ইত্যাদিতে ব্যবহৃত হয়।

ASCII ও EBCDIC কোড

ASCII (American Standard Code for Information Interchange) – ৭ বা ৮ বিটের মাধ্যমে ১২৮ বা ২৫৬ টি ক্যারেক্টার প্রকাশ করা যায়।

EBCDIC (Extended Binary Coded Decimal Interchange Code) – IBM কম্পিউটারে ব্যবহৃত ৮-বিটের একটি কোডিং পদ্ধতি।
আমেরিকান স্ট্যান্ডার্ড ইনস্টিটিউট ASCII কোড প্রকাশ করেছে, যা ব্যক্তিগত কম্পিউটার সহ বিভিন্ন কম্পিউটারে ব্যাপকভাবে ব্যবহৃত হয়। এই কোডিং পদ্ধতিতে 2 পাওয়ার ৮ = ১২৮টি বিভিন্ন কোড তৈরি করা যায়। ডেটা স্থানান্তরের জন্য প্যারিটি বিট ব্যবহার করার সময়, এর দৈর্ঘ্য বিশেষভাবে ৮ বিট বা ১ বাইট। IBM কোম্পানী EBCDIC নামে একটি নতুন ৮-বিট কোড তৈরি করেছে, যা তার IBM কম্পিউটারে ব্যবহারের জন্য আলাদা। তবে নাম ভিন্ন হলেও পদ্ধতি একই। ৭ বিটের ১২৮টি সজ্জায়, দুটি পদ্ধতি দুটি নামে কোড করা হয়েছে। অবশিষ্ট ৮ তম বিট অবশ্যই একটি প্যারিটি বিট হতে হবে। উদাহরণস্বরূপ, ASCII কোডিং পদ্ধতিতে, ৮ বিটের ১০১০০০০১-এ সজ্জাকে A বলা হয় কিন্তু EBCDIC পদ্ধতিতে, ১১০০০০০১-এ সজ্জাকে বলা হয় A। আমি আপনাকে আরও কয়েকটি উদাহরণ দিই।
 চিত্র: ASCII vs EBCDIC

কোডিং: BCD, ASCII ও EBCDIC

কম্পিউটারে তথ্য সংরক্ষণ ও আদান-প্রদানের জন্য বিভিন্ন ধরণের কোডিং পদ্ধতি ব্যবহার করা হয়। নিচে জনপ্রিয় তিনটি কোডিং পদ্ধতির ব্যাখ্যা দেওয়া হলো:

১. BCD (Binary Coded Decimal)

BCD হল একটি পদ্ধতি যেখানে প্রতিটি দশমিক সংখ্যা (০ থেকে ৯) ৪-বিট বাইনারি দ্বারা প্রকাশ করা হয়। অর্থাৎ, একটি দশমিক সংখ্যার প্রতিটি অঙ্ককে আলাদাভাবে বাইনারি রূপে প্রকাশ করা হয়।

উদাহরণ: দশমিক 59 → BCD = 0101 1001

২. ASCII (American Standard Code for Information Interchange)

ASCII হল একটি ৭-বিট বা ৮-বিট কোড, যা বর্ণ, সংখ্যা এবং কিছু নিয়ন্ত্রণ চিহ্ন সংরক্ষণে ব্যবহৃত হয়। এতে মোট ১২৮ টি স্ট্যান্ডার্ড ক্যারেক্টার আছে। যেমন:

• 'A' = 65 (01000001)
• 'a' = 97 (01100001)
• '0' = 48 (00110000)

৩. EBCDIC (Extended Binary Coded Decimal Interchange Code)

EBCDIC হল IBM কর্তৃক উন্নীত একটি ৮-বিট ক্যারেক্টার এনকোডিং পদ্ধতি। এটি মূলত মেইনফ্রেম কম্পিউটারে ব্যবহৃত হয়। ASCII এর চেয়ে ভিন্ন বিন্যাসে ক্যারেক্টার গুলি এনকোড করা হয়।

উদাহরণ: EBCDIC-এ 'A' = 11000001

এই কোডিং পদ্ধতিগুলোর মাধ্যমে কম্পিউটার সহজে বিভিন্ন ভাষা, সংখ্যা এবং প্রতীক বুঝতে পারে এবং এগুলো মেমোরিতে সংরক্ষণ করতে পারে।

উপসংহার:
সংখ্যা পদ্ধতি একটি গুরুত্বপূর্ণ অধ্যায় যা কম্পিউটারের প্রাথমিক কার্যপ্রণালী বুঝতে সাহায্য করে। এই অধ্যায়টি ভালোভাবে আয়ত্ত করলে কম্পিউটারের অভ্যন্তরীণ গাণিতিক কার্যকলাপ বুঝতে সুবিধা হবে।

সংখ্যা পদ্ধতি সম্পর্কিত সাধারণ প্রশ্নোত্তর (FAQ)

কম্পিউটারে সংখ্যা পদ্ধতি সম্পর্কিত সাধারণ প্রশ্নোত্তর (FAQ)