সাধারণ গণিত নবম দশম শ্রেণি (এসএসসি) পাঠ্য বইয়ের অনুশীলনী ৬.৩ এর ১০ নাম্বার অংকের সহজ সমাধান।
প্রমাণ কর যে, ত্রিভুজের মধ্যমাত্রয়ের সমষ্টি তার পরিসীমা অপেক্ষা ক্ষুদ্রতর।
 বিশেষ নির্বচন:
বিশেষ নির্বচন:
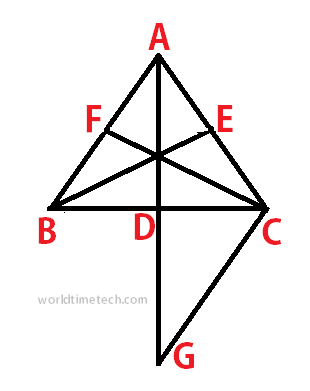
মনেকরি, ∆ABC এ BC, AC এবং AB বাহুতে মধ্যমা যথাক্রমে AD, BE এবং CF
প্রমাণ করতে হবে যে, AD + BE + CF < AB + BC + AC
অংকণঃ
AD – কে G পর্যন্ত এমনভাবে বর্ধিত করি যেন, AD = DG হয়। অতঃপর C, G যোগ করি।
প্রমাণ:
∆ABD এবং ∆CDG - এ BD = CD [ ∵ AD, BC বাহুতে মধ্যমা ]
AD = DG [অংকণ অনুসারে]
এবং অন্তর্ভূক্ত ∠ADB = অন্তর্ভূক্ত ∠CDG [বিপ্রতীপ কোণ] :
∴ ∆ABD ≅ ∆CDG
∴ AB = CG
আবার, ∆ACG এ AC + CG > AG
বা, AC + AB > AD + DG [∵ AB = CC এবং AG = AD + DG)
বা, AC + AB > AD + AD [∵ DG = AD]
বা, AB+ AC > 2AD --------- (1)
অনুরূপভাবে দেখানো যায়,
AB+ BC > 2BE ----------(2)
এবং BC + AC > 2CF ----------(3)
এখন (1) নং, (2) নং এবং (3) নং অসমতা যোগ করে পাই,
AB + AC + AB+ BC + BC + AC > 2AD + 2BE + 2CF
বা, 2AB + 2BC + 2AC > 2AD + 2BE + 2CF
বা, 2(AB + BC + AC) > 2 (AD + BE + CF)
বা, (AB+ BC + AC) > (AD + BE + CF) [উভয়পক্ষকে 2 দ্বারা ভাগ করে।]
∴ AD + BE + CF < AB + BC + AC
(প্রমাণিত)
proman koro je, trivujer modhomatrayer somosti tar porisima opekha khudrotor

